Vad är egentligen reella tal?

Inom matematiken kan alla tal delas inom olika talmängder. Dessa olika talmängder är naturliga tal, heltal, rationella tal, reella tal och komplexa tal. De är också delmängder av varandra och de reella talen innefattar även de naturliga talen, heltal och de rationella talen.

I detta inlägget kommer du få reda på vad de reella talen är i matematiken, samt vilka tal som inte är reella. När man börjar läsa om de olika talmängderna i matematiken kan det vara rörigt, men jag hoppas kunna förtydliga det i detta inlägget.

Vad är reella tal?

Reella tal innefattar alla tal som kan skrivas på tallinjen. Detta är de naturliga talen, alla heltal, alla rationella tal samt alla tal som inte kan skrivas som ett bråk såsom pi. Inom matematiken brukar de reella talen betecknas med bokstaven R.

Nedan ser du en förklarande bild på vad reella tal är. Som du ser är rationella, heltal och naturliga tal delmängder till reella tal. Denna bilden visar att naturliga tal, heltal och rationella tal också är reella tal.

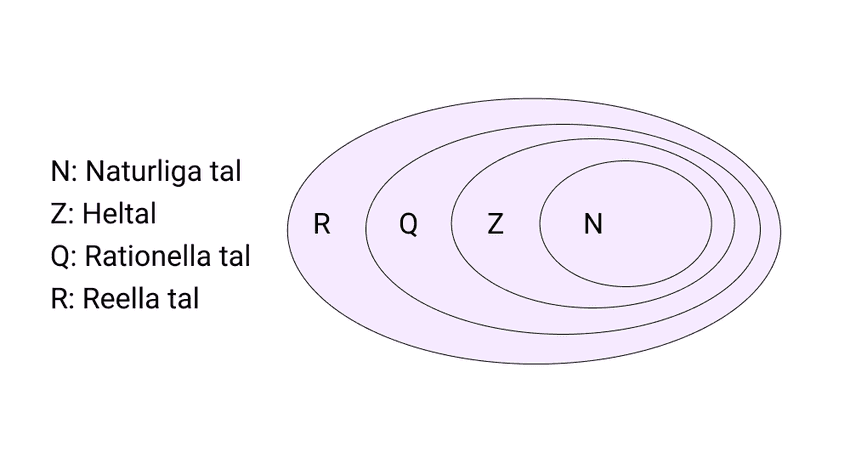
Exempel på reella tal är 0, 1, -5, 1/2 och $\pi$. Dessa olika talen kan också delas in i de andra olika talmängderna. Exempelvis är 0 och 1 även naturliga tal, -5 är ett heltal, 1/2 är ett rationellt tal medan pi är ett reellt tal.

Man stöter ofta på reella tal när man blir introducerad till andragradsekvationer i matematiken. Detta beror på att andragradsekvationer både kan ha reella och komplexa lösningar.

En komplex lösning har däremot inget med att göra att det är svårt, utan komplexa tal är sorts tal som inte kan skriva på tallinjen. Komplexa tal innehåller både realdel och en imaginär del.

Hur skiljer sig komplexa tal från reella?

Det finns tal som inte är reella och de kallas för komplexa tal. Det är tal som inte kan skrivas på tallinjen, och är en utvidgning av de reella talen.

Ett komplext tal kan skrivas som “$z = a + ib$” där talet a är realdelen, det reella talet b är imaginärdelen och i är den i maginära enheten med egenskapen $i^2 = -1$.

Det är under gymnasiet som man först stöter på de komplexa talen när man ska lösa andragrads-ekvationer. Ett exempel på en ekvation som saknar reella lösningar är $x^2=−4$. Detta beror på att det inte finns något reellt tal som blir $-4$ när man tar kvadraten av det. Däremot har ekvationen komplexa lösningar vilket är $-2i$ och $2i$.

När saknar andragradsekvationer reella lösningar?

Om en andragradsekvationer har reella lösning eller inte beror ekvationens diskriminant, vilket är uttrycket under rottecknet för PQ-formeln. Uttrycket under rottecknet är:

$(\frac{p}{2}^2 - q)$

Om detta uttrycket ovan är större än noll kommer andragradsekvationen ha två reella lösningar. Om uttrycket är lika med 0 kommer det finnas en reell lösning, och om uttrycket är mindre än 0 kommer ekvationen sakna reella lösningar. Detta beror att talet blir komplext om man tar roten ur ett negativt tal.

$(\frac{p}{2}^2 - q ) > 0 \implies 2 \text{ reella lösningar}$

$(\frac{p}{2}^2 - q) = 0 \implies 1 \text{ reell lösning}$

$(\frac{p}{2}^2 - q) < 0 \implies 0 \text{ reella lösningar}$

Ovan kan du se en sammanfattning utav de tre olika fallen.

Andra vanliga frågor

Nedan går jag igenom ett antal andra vanliga frågor om reella tal som jag hoppas kan vara till hjälp för dig.

Vilka tal är icke reella?

Om ett komplext tal saknar en reell del kallas det för ett rent imaginärt tal. Ett exempel på ett rent imaginärt tal är $x_1=4i$ eftersom talet helt saknar en reell del. Normalt sätt kan de komplexa talet innehålla både en reell och en imaginär del.

Kan ett reellt tal vara negativt?

Ja, eftersom reella tal innefattar alla tal som kan skrivas på tallinjen kan ett reellt tal vara negativt. Två exempel på reella tal är -215,3 och 3,53.

Vilken symbol har de reella talen?

Mängden av alla reella talen betecknas vanligtvis med symbolen ℝ eller R. Inom mängden R innefattas alla de tal som vi vanligtvis menar med tal.

Vad är en reell dubbelrot?

Om diskriminanten lika med noll kommer andragradsekvationen endast att ha en reell lösning och då kallas det för en dubbelrot.